Faktorisierte Form (Produktform) einer quadratischen Funktion
Eine quadratische Funktion liegt in ihrer faktorisierten Form vor, wenn sie soweit möglich in Linearfaktoren zerlegt ist. Einfacher gesagt, handelt es sich bei der faktorisierten Form um die Produktform der Parabel. Die einzelnen Faktoren des Produkts sind die gerade erwähnten Linearfaktoren, welche die Form 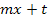 haben, also kein
haben, also kein  oder eine noch höhere Potenz von x enthalten. Eine quadratische Funktion besitzt maximal zwei Linearfaktoren.
oder eine noch höhere Potenz von x enthalten. Eine quadratische Funktion besitzt maximal zwei Linearfaktoren.
Faktorisierte Form (Produktform) einer Parabel: 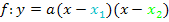
Dabei stellen 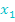 und
und 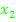 die x-Koordinaten der Nullstellen der Parabel (Schnittpunkte des Graphen mit der x-Achse) dar. Daher gibt es die faktorisierte Form nur bei Parabeln, die Nullstellen besitzen.
die x-Koordinaten der Nullstellen der Parabel (Schnittpunkte des Graphen mit der x-Achse) dar. Daher gibt es die faktorisierte Form nur bei Parabeln, die Nullstellen besitzen.
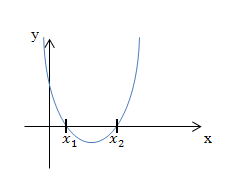
Abb.:Parabel mit zwei Nullstellen (Schnittpunkte mit der x-Achse)
Bsp.: 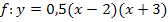 faktorisierte Form der Funktion
faktorisierte Form der Funktion 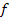
![]()
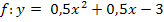 ausmultiplizierte/allgemeine Form der Funktion
ausmultiplizierte/allgemeine Form der Funktion 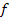
Aus der faktorisierten Form von 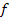 lassen sich die Nullstellen ganz leicht ermitteln:
lassen sich die Nullstellen ganz leicht ermitteln:
Zur Erinnerung: Nullstellen berechnet man, indem man den Funktionsterm 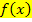 gleich Null setzt bzw. für y die Zahl Null einsetzt. (Da die Nullstellen auf der x-Achse liegen, muss y = 0 bzw. gleich Null setzt bzw. für y die Zahl Null einsetzt. (Da die Nullstellen auf der x-Achse liegen, muss y = 0 bzw. 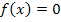 sein;alle Punkte, die auf der x-Achse liegen haben schließlich die y-Koordinate 0.) sein;alle Punkte, die auf der x-Achse liegen haben schließlich die y-Koordinate 0.) |
Nullstellen: 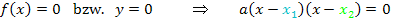
Da ein Produkt gleich Null ist, wenn einer der Faktoren gleich Null ist, kann man die Klammern einfach einzeln gleich Null setzen.
Auf unser Beispiel von oben bezogen, bedeutet das:
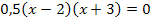
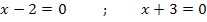

Man braucht also nur bei den Zahlen in den Klammern jeweils das Vorzeichen umdrehen und schon hat man die x-Koordinaten der beiden Nullstellen.

