Quadratische Ergänzung (zur Scheitelberechnung)
Mit Hilfe der sogenannten quadratischen Ergänzung lässt sich die allgemeine Form einer Parabel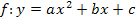 
in die Scheitelform 
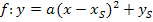umwandeln. Aus der Scheitelform kann der Scheitel dann bequem abgelesen werden. Die quadratische Ergänzung ist allerdings ziemlich aufwendig und für die meisten Schüler nicht einfach zu lernen. Beim Erlernen der quadratischen Ergänzung soll dir die unten gezeigte Tabelle helfen. Auf der linken Seite der Tabelle findest du eine allgemeine Anleitung für die einzelnen Schritte zur Scheitelberechnung durch quadratische Ergänzung und parallel dazu ein konkretes Beispiel auf der rechten Seite.
| Geg.: |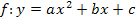
Geg.:  |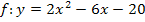
| Anleitung zur quadratischen Ergänzung
zur Berechnung der Scheitelkoordinaten |
Konkretes Beispiel |
| 1. Schritt:a komplett ausklammern
d.h. jeden Faktor einzeln durch a teilen Verwende am besten eckige Klammern! Runde Klammern brauchen wir später noch. |
|
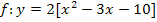
| 2. Schritt:Quadratisch ergänzen, um eine binomische Formel herzustellen
d.h. man nimmt die Zahl vor dem x (ohne Vorzeichen) halbiert und quadriert sie;das addiert man zuerst und subtrahiert dann gleich wieder, damit sich an dem Funktionsterm nichts ändert. (Man muss immer zuerst + und erst danach – schreiben, da andernfalls keine binomische Formel entsteht. Weder die erste noch die zweite binomische Formel haben hinten ein Minus!) Zur Wiederholung: 1. Binom: 2. Binom: |
Die Zahl vor dem x (ohne Vorzeichen) ist hier 3
Halbiert Quadriert Zuerst + danach – So erhalten wir:
Innerhalb der runden Klammer steht hier die zweite binomische Formel, da vor 3x ein Minus steht. (Hätte vor 3x ein Plus gestanden, hätte sich die erste binomische Formel ergeben.) |
| 3. Schritt:Binomische Formel umformen |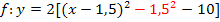 
Ist dir dieser Schritt nicht klar, wiederhole bitte das Rechnen mit Binomischen Formeln! |
| 4. Schritt:Zusammenfassen so weit möglich |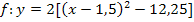 
|
| 5. Schritt: a (= Zahl vor der eckigen Klammer) in die eckige Klammer hinein multiplizieren, d.h. a vor die runde Klammer schreiben und a mit der hinteren Zahl (in der eckigen Klammer) multiplizieren.
Achtung: a nicht in die runde Klammern hinein multiplizieren! Das Quadrat bezieht sich nur auf die runde Klammer, aber nicht auf a. Deshalb wäre es falsch, a in die runde Klammer hinein zu multiplizieren. Nach diesem Schritt liegt die Scheitelform der Parabel vor. Scheitelform |
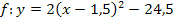
Das ist die Scheitelform der Parabel. Aus ihr kann nun der Scheitel direkt abgelesen werden. |
| 6. Schritt:Scheitelkoordinaten ablesen
Bei der Zahl in der Klammer das Vorzeichen umdrehen und du hast die x-Koordinate des Scheitels Die Zahl hinter der Klammer entspricht der y-Koordinate des Scheitels |
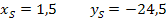
Scheitel S(1,5| -24,5) |
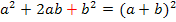
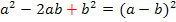
1,5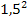
.
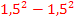
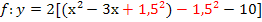
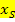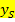. Dabei das Vorzeichen lassen, wie es ist.
