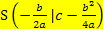Herleitung der Formel zur Scheitelberechnung
Um die folgende Herleitung der Formel Scheitel S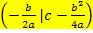 
nachvollziehen zu können, ist es unerlässlich, dass du die Quadratische Ergänzung (zur Scheitelberechnung) beherrschst.
Wir gehen nun von der allgemeinen Form der Parabel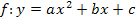 
aus und verwenden das Schema, das bei der quadratischen Ergänzung zur Scheitelberechnung gezeigt wurde. Es werden für a, b und c im Folgenden natürlich keine konkreten Zahlen verwendet;es soll schließlich eine allgemeine Formel entstehen.
Um die ziemlich komplizierte Rechnung übersichtlicher zu gestalten, findet sich in der folgenden Tabelle links noch einmal die Anleitung zur quadratischen Ergänzung in ihren einzelnen Schritten und rechts parallel dazu die allgemeine Rechnung.
Gesucht: Scheitel  ) |
Geg.:  |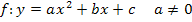
| Anleitung zur quadratischen Ergänzung
zur Berechnung der Scheitelkoordinaten |
Allgemeine Rechnung: |
| 1. Schritt:a ausklammern
d.h. jeden Faktor einzeln durch a teilen Verwende am besten eckige Klammern! Runde Klammern brauchen wir später noch. |
|
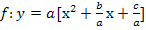
| 2. Schritt:Quadratisch ergänzen, um eine binomische Formel herzustellen
d.h. man nimmt die Zahl vor dem x (ohne Vorzeichen) halbiert und quadriert sie;das addiert man zuerst und subtrahiert dann gleich wieder, damit sich an dem Funktionsterm nichts ändert. (Man muss immer zuerst + und erst danach – schreiben, da andernfalls keine binomische Formel entsteht. Weder die erste noch die zweite binomische Formel haben hinten ein Minus!) Zur Wiederholung: 1. Binom: 2. Binom: |
Die Zahl vor dem x (ohne Vorzeichen) ist 
Halbiert Quadriert Zuerst + danach So erhalten wir:
Innerhalb der runden Klammer steht nun die erste binomische Formel, da vor |
| 3. Schritt:Binomische Formel umformen |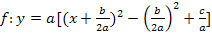 
Ist dir dieser Schritt nicht klar, wiederhole bitte das Rechnen mit Binomischen Formeln! |
| 4. Schritt:Vereinfachen so weit möglich |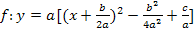 
|
| 5. Schritt: a in die eckige Klammer hinein multiplizieren, d.h. a vor die runde Klammer schreiben und a mit jedem restlichen Ausdruck (in der eckigen Klammer) multiplizieren. a kann dann jeweils weggekürzt werden.
Achtung: a nicht in die runde Klammern hinein multiplizieren! Das Quadrat bezieht sich nur auf die runde Klammer, aber nicht auf a. Deshalb wäre es falsch, a in die runde Klammer hinein zu multiplizieren. Nach diesem Schritt liegt die Scheitelform der Parabel vor. Scheitelform |
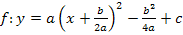
Wir drehen jetzt noch die Reihenfolge der beiden letzten Ausdrücke um.
Das ist die allgemeine Scheitelform der Parabel. Aus ihr kann nun der Scheitel in seiner allgemeinen Form abgelesen werden. |
| 6. Schritt:Scheitelkoordinaten ablesen
Bei dem Ausdruck in der Klammer das Vorzeichen umdrehen und du hast die x-Koordinate des Scheitels Der Ausdruck hinter der Klammer entspricht der y-Koordinate des Scheitels |
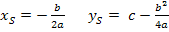
Scheitel Nun ist die Formel für den Scheitel hergeleitet. |
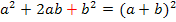
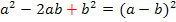
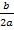
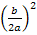
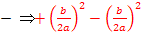
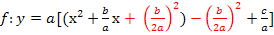
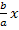ein Plus steht. (Hätte vor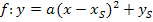 
.
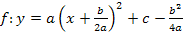
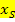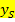. Dabei das Vorzeichen lassen, wie es ist.
