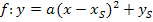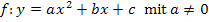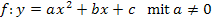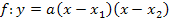Quadratische Funktionen (Parabeln)
Im Folgenden findest du die wichtigsten Dinge rund um das Thema quadratische Funktionen und ihre Graphen, die Parabeln, an Hand von vielen Beispielen erklärt.
| Übersicht über den Inhalt dieses Kapitels:
· Was ist überhaupt eine quadratische Funktion bzw. eine Parabel? Ist die Parabel nach oben oder nach unten geöffnet? Liegt eine Normalparabel vor oder ist sie breiter bzw. schmäler? Alles Wichtige über Funktionen der Form
· Das Wichtigste über die Scheitelform einer Parabel: · Berechnung des Scheitelpunkts einer Funktion des Typs · Nullstellen einer quadratischen Funktion · Wie kann man Parabeln zeichnen? · Wie ermittelt man die Wertemenge und Symmetrieachse? · Wie zerlegt man eine quadratische Funktion in ihre einzelnen Linearfaktoren? Eine Antwort darauf erhältst du im Kapitel: Faktorisierte Form (Produktform) einer quadratischen Funktion · Wie man die Funktionsgleichung einer Parabel z.B. mit drei gegebenen Punkten oder einem Punkt und dem Scheitel ermittelt, wird erklärt im Kapitel: Funktionsgleichung einer Parabel aufstellen · Wie schneidet man eine Parabel mit einer Gerade? Wie weist man rechnerisch nach, dass eine Gerade Tangente an eine Parabel ist? Solche Dinge werden erklärt im Kapitel Lagebeziehungen zwischen Parabel und Gerade. · Wie schneidet man zwei Parabeln mit einander? Wie ermittelt man rechnerisch die Anzahl der gemeinsamen Punkte zweier Parabeln? Darum geht es im Kapitel Lagebeziehungen zwischen zwei Parabeln. · Parabelscharen (Kommt in der Funktionsgleichung neben x und y noch ein anderer Buchstabe (z.B. a oder t), ein sogenannter Parameter, vor, liegt eine Funktionenschar vor.) Für Realschüler eines nicht-mathematischen Zweiges nicht Schulstoff! Für alle anderen Schüler sind Scharparabeln von großer Wichtigkeit, da Scharfunktionen häufig Prüfungsstoff sind. |

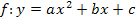 im Kapitel:
im Kapitel: