Rechnerische Lösungsverfahren von Bruchgleichungen
Bevor man beginnt eine Bruchgleichung rechnerisch zu lösen, muss immer erst die Definitionsmenge der Gleichung ermittelt werden. Wie schon im Kapitel Definitionsmenge einer Bruchgleichung ausführlich erläutert, kann die Lösungsmenge einer Bruchgleichung nämlich von der Definitionsmenge abhängen. Wir werden dazu weiter unten noch konkrete Beispiele besprechen.
Sagen wir ´mal, du hast von einer gegebene Bruchgleichung bereits die Definitionsmenge ermittelt und sollst die Gleichung jetzt nach x auflösen. Wie geht das denn überhaupt? Im Prinzip ist das nicht so schwer:Du überlegst dir den Hauptnenner der gesamten Gleichung und multiplizierst dann damit. Dadurch fällt dann nämlich der Nenner auf beiden Seiten der Gleichung weg und es entsteht eine einfache Gleichung, die auf jeden Fall kein x mehr im Nenner enthält. In der 8. Klasse entsteht dabei immer eine lineare Gleichung;also eine Gleichung bei der letztendlich kein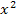 
mehr vorkommt. 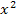muss sich zumindest am Ende wegheben;sonst hast du dich mit größter Wahrscheinlichkeit verrechnet, da Gleichungen mit 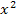erst Stoff der 9. Klasse (G8) sind. In der 8. Klasse musst du solche Gleichungen (bis auf einige wenige Ausnahmen, die sehr einfache Sonderfälle darstellen) noch nicht lösen können. Ab der 9. Klasse kommen dann aber auch Bruchgleichungen, die zu Quadratischen Gleichungen führen.
