Graphisches Lösungsverfahren von Bruchgleichungen

In diesem Kapitel werden Vorkenntnisse in den Themengebieten Gebrochenrationale Funktionen (Hyperbeln) und Lineare Funktionen (Geraden) vorausgesetzt. Wenn du dich bei den gebrochenrationalen Funktionen (d.h. Funktionen mit x im Nenner) und ihren Graphen, den Hyperbeln, noch nicht sicher fühlst, bearbeite unbedingt zuerst das Kapitel Gebrochenrationale Funktionen (Hyperbeln)! Wenn ihr die gebrochenrationalen Funktionen in der Schule noch gar nicht besprochen habt, musst du das im Folgenden gezeigte graphische Verfahren zur Lösung von Bruchgleichungen nicht können. Dann reicht es für dich die Rechnerischen Lösungsverfahren von Bruchgleichungen zu beherrschen. Dies gilt beispielsweise für alle Schüler einer Realschule (R6 nicht mathematischer Zweig). Besuchst du allerdings ein Gymnasium (G8) oder eine Realschule (R6 mathematischer Zweig) in Bayern, gehört das unten besprochene graphische Verfahren zu deinem Schulstoff.

Du weißt sicher vom Prinzip her, wie der Schnittpunkt zweier Funktionen berechnet wird:Die beiden Funktionen müssen gleichgesetzt werden. Löst man die entstandene Gleichung nach x auf, erhält man die x-Koordinate(n) des Schnittpunkts bzw. der Schnittpunkte der beiden Funktionsgraphen.

Eine Bruchgleichung kann somit auch als eine Gleichung angesehen werden, die durch das Gleichsetzen einer gebrochenrationalen Funktion mit einer weiteren Funktion entstanden ist. Die Lösung einer Bruchgleichung entspricht daher der x-Koordinate des Schnittpunkts einer gebrochenrationalen Funktion mit einer zweiten Funktion. Dabei kann es sich bei der zweiten Funktion ebenfalls um eine gebrochenrationale Funktion, also wieder um eine Funktion mit x im Nenner, oder um eine Polynomfunktion, z.B. eine Gerade oder quadratische Funktion (Parabel), handeln. (Eine Polynomfunktion hat kein x im Nenner.) Das hängt natürlich davon ab, ob auf beiden Seiten der Gleichung x im Nenner vorkommt oder nicht.

Kommt auf beiden Seiten der Gleichung x im Nenner vor, dann muss der Schnittpunkt zweier gebrochenrationaler Funktionen, also zweier Hyperbeln, ermittelt werden. Ansonsten wird eine gebrochenrationale Funktion mit einer Polynomfunktion geschnitten.

Da die Parabeln erst Stoff der 9. Klasse (G8 und R6 math. Zweig) sind, die Bruchgleichungen aber bereits in der 8. Klasse (G8) zum ersten Mal behandelt werden, verzichten wir hier erst einmal auf den Schnitt gebrochenrationaler Funktionen mit Quadratischen Funktionen (Parabeln), damit der anfängliche Teil des Kapitels auch von Schülern genutzt werden kann, die noch keine Parabeln gelernt haben, wie z.B. Schülern der 8. Klasse (G8).

Erst am Ende des Kapitels folgt ein kleinerer Teil, der dann speziell den Schnitt gebrochenrationaler Funktionen mit Parabeln behandelt. Dieser Teil ist entsprechend gekennzeichnet.

Anmerkung:

Nicht jede Bruchgleichung lässt sich gut mittels des oben beschriebenen graphischen Verfahrens lösen. So kann es beispielsweise zu Problemen kommen, da sich der Schnittpunkt nicht gut ablesen lässt, da die beiden Graphen in der Umgebung des Schnittpunkts nahezu parallel verlaufen. Dann ist es nicht möglich die x-Koordinate des gemeinsamen Punktes mit ausreichender Genauigkeit aus der Zeichnung abzulesen. Bei solchen Aufgaben empfiehlt es sich auf einen rechnerischen Lösungsweg zurückzugreifen. Außerdem kann der Schnittpunkt außerhalb des gezeichneten Bereichs liegen. Dann kann allerdings ein anderer Ausschnitt des Graphen gezeichnet oder ein größerer Maßstab gewählt werden. Jedoch eignen sich wirklich nicht alle Bruchgleichungen für das graphische Lösungsverfahren. Die im Folgenden gezeigten Beispiele sind speziell für das graphische Verfahren ausgesucht worden. Wende das graphische Verfahren nur bei Aufgaben mit Bruchgleichungen an, wenn extra der graphische Weg verlangt ist! Manchmal ist es auch geschickt, mittels des graphischen Verfahrens erst einmal festzustellen, ob überhaupt eine Lösung existieren kann, oder ob die Lösungsmenge sowieso leer ist, da die beiden Funktionen gar keine gemeinsamen Punkte besitzen. Falls ein Schnittpunkt existiert, dessen Koordinaten jedoch schlecht abzulesen sind, wendet man dann ein rechnerisches (algebraisches) Verfahren an und ermittelt so die gesuchte Lösung durch Rechnung. Manche Bruchgleichungen lassen sich erst nach einer geeigneten Umformung graphisch lösen, andere Bruchgleichungen lassen sich direkt oder nach einer Umformung graphisch lösen, so dass zu einer Bruchgleichung verschiedene graphische Lösungswege möglich sind.

So, nun schauen wir uns erst ´mal ein paar Beispiele an.

1. Bsp.:

Löse die folgende Gleichung graphisch!

Lösung:

Die gegebene Bruchgleichung könnte entstanden sein durch das Gleichsetzen der beiden gebrochenrationalen Funktionen f(x) = und h(x) . Die Gleichung würde also bei der Schnittpunktberechnung der beiden Funktionen f(x) und h(x) entstehen. Da hier eine graphische Lösung verlangt ist, zeichnen wir die Graphen der beiden Funktionen in ein gemeinsames Koordinatensystem und lesen dann die x-Koordinate des Schnittpunkts ab. Nun stellt sich allerdings die Frage, wie man die Graphen der Funktionen am geschicktesten zeichnen kann. Beide Funktionen sind gebrochenrational, weil beide Funktionsgleichungen die Variable x im Nenner enthalten. Der Graph einer gebrochenrationalen Funktion ist bekanntlich eine Hyperbel. Den Verlauf von Hyperbeln kann man grob mit Hilfe ihrer Asymptoten skizzieren. Nun kommt es darauf an, dass du sofort an Hand der Funktionsgleichungen die Asymptoten und den ungefähren Verlauf der beiden Graphen erkennen kannst. Du solltest elementare gebrochenrationale Funktionen – das sind Funktionen des Typs f(x) = (mit und n ℕ) – auch ohne Wertetabelle skizzieren können! Wie das geht, wird ausführlich im Kapitel Gebrochenrationale Funktionen (Hyperbeln) erklärt. In diesem Kapitel wird das nur noch kurz wiederholt. Wir benötigen vor allem die Gleichungen der Asymptoten, um die Graphen skizzieren zu können. Du weißt hoffentlich noch:Asymptoten sind Geraden, an die sich der Graph anschmiegt, die er aber nicht schneidet.

Kurze Wiederholung:

Eigenschaften von Funktionen des Typs f(x) = (mit und n ℕ)

Asymptoten:

Senkrechte Asymptote: x = – b

(D.h. die senkrechte Asymptote liegt bei der Definitionslücke.)

Waagrechte Asymptote: y = c

(D.h. die Zahl hinter dem Bruch gibt an, wo die waagrechte Asymptote liegt.)

Symmetrie:

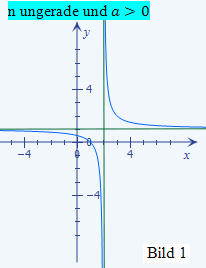
Ist die Potenz n der Klammer im Nenner ungerade, ist der Graph der Funktion punktsymmetrisch zum Schnittpunkt der beiden Asymptoten (- b;c). Der Verlauf des Graphen hängt dabei noch vom Vorzeichen des Bruchs ab:

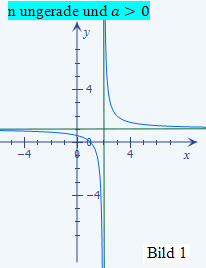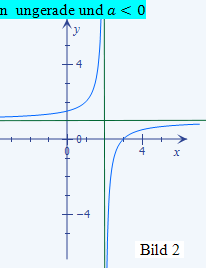Ist die Potenz n der Klammer im Nenner gerade, ist der Graph der Funktion achsensymmetrisch zur senkrechten Asymptote x = – b.

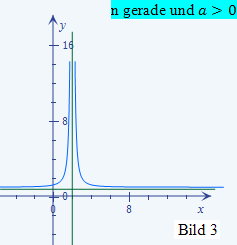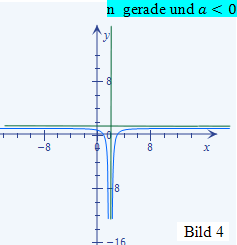Nun wieder zurück zu unseren beiden Funktionen f(x) = und h(x) . Was kann man nun ohne Wertetabelle über die Graphen dieser beiden Funktionen nur durch Betrachten der Funktionsgleichungen aussagen?

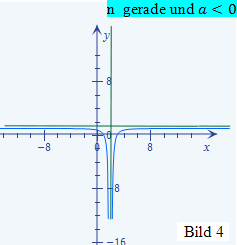
Schauen wir uns die erste Funktion f(x) = an. Die Definitionslücke dieser Funktion liegt bei x = 4. Das ist somit auch die Gleichung der senkrechten Asymptote. Die waagrechte Asymptote hat die Gleichung y = 2. Wegen der geraden Potenz (n = 2) der Klammer im Nenner ist die Funktion achsensymmetrisch zu ihrer senkrechten Asymptote, also zu der Gerade x = 4. Wegen des negativen Vorzeichens des Bruchs ( ) und der geraden Potenz ähnelt der Graph der Funktion f(x) dem im Bild 4 gezeigten Graph.

Die zweite Funktion h(x) besitzt die Definitionslücke x = 2. Daher liegt die senkrechte Asymptote dieser Funktion bei x = 2. Die waagrechte Asymptote hat die Gleichung y = 3. Im Nenner des Bruchs steht keine Klammer, also eigentlich keine Potenz. Man kann sich jedoch eine Klammer mit der Potenz 1 hinzu denken. Somit liegt hier eine ungerade Potenz (n = 1) vor. Der Bruch hat ein negatives Vorzeichen, also gilt . Deswegen ähnelt der Graph der Funktion h(x) dem im Bild 2 dargestellten Graph.

Nun können die beiden Funktionen bereits grob skizziert werden. Für eine genaue Zeichnung benötigt man jedoch zumindest ein paar Funktionswerte, sonst wird die Zeichnung zu ungenau. Am besten ist es, wenn du vorweg eine grobe Skizze anfertigst. Dann kannst du nämlich schon einmal ungefähr erkennen, wo sich die beiden Graphen schneiden. Nur in diesem Bereich musst du die Funktionen wirklich genau zeichnen. D.h. in diesem Bereich solltest du einige Funktionswerte berechnen. Wenn du dir die Arbeit, eine grobe Skizze zu machen, sparen willst, kannst du auch einfach jeweils eine Wertetabelle für x [- 7;7] und einer Schrittweite von △x = 0,5 mit dem Taschenrechner erstellen und die Graphen mit diesen Werten zeichnen. In den meisten Fällen wird der Schnittpunkt in diesem Bereich liegen. (Mit einem Taschenrechner, der Wertetabellen berechnen kann, geht das ja ganz schnell. Mit einem anderen Taschenrechner ist das natürlich viel zu viel Arbeit. Dann machst du lieber vorher die grobe Skizze und überlegst dir, welche Funktionswerte wirklich wichtig sind und deshalb unbedingt berechnet werden müssen.)

Versuche nun die beiden Graphen selbst in ein gemeinsames Koordinatensystem zu zeichnen und die x-Koordinate des Schnittpunkts so genau wie möglich abzulesen!

Platzbedarf:

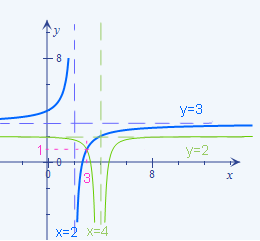
Abb.:Graphen der Funktionen f(x) = und h(x) mit ihrem Schnittpunkt (3|1)

In der Zeichnung ist der Schnittpunkt der beiden Graphen gut zu erkennen. Die x-Koordinate des Schnittpunkts lautet:x = 3

Somit ist die Lösung der gegebenen Bruchgleichung x = 3.

Wir machen noch die Probe, d.h. wir setzen für x den Wert 3 in die Gleichung ein.

Hier noch einmal die Gleichung:

Probe für x = 3:

(wahr)

Wir haben mit x = 3 also wirklich exakt die Lösung der Gleichung ermittelt.

Anmerkung:Die Gleichung hätte auch auf eine andere Weise graphisch gelöst werden. Man hätte die Gleichung nämlich auch zuerst umformen können und hätte so zwei andere Terme auf den beiden Seiten der Gleichung, also zwei andere Funktionen erhalten, deren Schnittpunkt allerdings unverändert bei x = 3 liegt. Beispielsweise wäre auch folgender Lösungsweg korrekt:

|

f*(x) = h*(x) =

Die Funktion f*(x) hat ihre Definitionslücke bei x = 4 und daher auch die senkrechte Asymptote x = 4. Die x-Achse y = 0 ist waagrechte Asymptote dieser Funktion. Der Graph der Funktion f*(x) ergibt sich aus dem Graph der Funktion f(x) durch Verschiebung um 2 nach unten. (Die Funktion f(x) hat ja auch die senkrechte Asymptote x = 4, aber die waagrechte Asymptote y = 2.)

Die Funktion h*(x) hat ihre Definitionslücke bei x = 2 und daher auch die senkrechte Asymptote x = 2. Die Gerade y = 1 ist waagrechte Asymptote dieser Funktion. Der Graph der Funktion h*(x) ergibt sich aus dem Graph der Funktion h(x) durch Verschiebung um 2 nach unten. (Die Funktion h(x) hat ja ebenfalls die senkrechte Asymptote x = 2, aber die waagrechte Asymptote y = 3.)

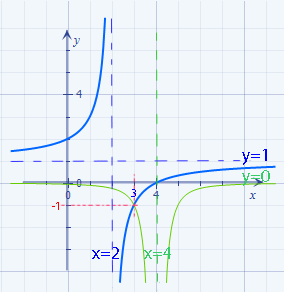
Abb.:Graphen der Funktionen f*(x) = und h*(x) mit ihrem Schnittpunkt (3|-1)

Die beiden Funktionen f*(x) und h*(x) ergeben sich beide jeweils durch eine Verschiebung von f(x) bzw. h(x) um 2 nach unten. Vergleiche dazu auch die an der Gleichung vorgenommene Äquivalenzumformung! Es wurde auf beiden Seiten der Gleichung 2 subtrahiert. Das entspricht eben einer Verschiebung von f(x) und h(x) um jeweils 2 nach unten. Da ja beide Funktionen f(x) und h(x) gleichmäßig um 2 nach unten verschoben werden, ändert sich an der x-Koordinate des Schnittpunkts nichts. Die x-Koordinate des Schnittpunkts ist immer noch x = 3. Das war ja auch zu erwarten, denn es handelt sich schließlich noch immer um die Lösung der ursprünglichen Bruchgleichung.

An Stelle der gerade eben gezeigten Äquivalenzumformung, hätte beispielsweise genauso gut auf beiden Seiten 3 subtrahiert werden können.

|

f**(x) = h**(x) =

Die Funktion f**(x) hat ihre Definitionslücke bei x = 4 und daher auch die senkrechte Asymptote x = 4. Die Parallele zur x-Achse y = – 1 ist waagrechte Asymptote dieser Funktion. Der Graph der Funktion f**(x) ergibt sich aus dem Graph der Funktion f(x) durch Verschiebung um 3 nach unten. (Die Funktion f(x) hat schließlich auch die senkrechte Asymptote x = 4, aber die waagrechte Asymptote y = 2.)

Die Funktion h**(x) hat ihre Definitionslücke bei x = 2 und daher auch die senkrechte Asymptote x = 2. Die Gerade y = 0, also die x-Achse, ist waagrechte Asymptote dieser Funktion. Der Graph der Funktion h**(x) ergibt sich aus dem Graph der Funktion h(x) durch Verschiebung um 3 nach unten. (Die Funktion h(x) hat ja ebenfalls die senkrechte Asymptote x = 2, aber die waagrechte Asymptote y = 3.)

Die beiden Funktionen f**(x) und h**(x) ergeben sich beide jeweils durch eine Verschiebung von f(x) bzw. h(x) um 3 nach unten. Vergleiche dazu die an der Gleichung vorgenommene Äquivalenzumformung! Es wurde auf beiden Seiten der Gleichung 3 subtrahiert. Das entspricht einer Verschiebung von f(x) und h(x) um jeweils 3 nach unten. Da ja beide Funktionen f(x) und h(x) gleichmäßig um 3 nach unten verschoben werden, ändert sich an der x-Koordinate des Schnittpunkts nichts. Die x-Koordinate des Schnittpunkts ist immer noch x = 3. Das hast du bestimmt erwartet, denn die x-Koordinate des Schnittpunkts von f**(x) und h**(x) ist schließlich noch immer die Lösung der ursprünglichen Bruchgleichung.

Die Graphen der Funktionen f**(x) und h**(x) sind nicht mehr abgebildet;du kannst sie sicher alleine zeichnen. Das wäre eine gute Übung für dich! Zu deiner Kontrolle kannst du wieder die x-Koordinate des Schnittpunkts verwenden:Er muss wieder x = 3 sein.

Bei jeder gleichmäßigen Verschiebung der beiden Funktionen f(x) und h(x) nach oben oder unten bleibt die x-Koordinate des Schnittpunkts unverändert. Eine Äquivalenzumformung führt zwar zu anderen Funktionen;die x-Koordinate des Schnittpunkts ändert sich dabei aber nicht. Du kannst das mit beliebigen Äquivalenzumformungen der Gleichung selbst ausprobieren. Immer wird die x-Koordinate des Schnittpunkts unverändert bleiben. Du kannst also ruhig eine gegebene Bruchgleichung zuerst durch geeignete Umformungen vereinfachen und erst danach das graphische Verfahren anwenden.

2. Bsp.:

Löse die folgende Gleichung graphisch!

Lösung:

Bei der vorliegenden Gleichung handelt es sich wieder um eine Bruchgleichung, da im Nenner die Lösungsvariable x auftritt. Die gegebene Bruchgleichung könnte z.B. entstanden sein durch das Gleichsetzen der beiden gebrochenrationalen Funktionen f(x) = und h(x) . Die Gleichung würde also bei der Schnittpunktberechnung der Funktionen f(x) und h(x) entstehen. Wir wenden also wieder das oben beschriebene Verfahren zur graphischen Lösung von Bruchgleichungen an:Die linke und die rechte Seite der Gleichung werden als einzelne Funktionen angesehen, die miteinander geschnitten werden.

Du brauchst also nur die beiden Funktionen f(x) = und h(x) in ein gemeinsames Koordinatensystem einzuzeichnen und die x-Koordinate des Schnittpunkts aus der Zeichnung abzulesen. Probiere es doch gleich ´mal selbst! Diese Aufgabe ist ja ganz ähnlich wie das vorherige Beispiel.

Brauchst du doch noch etwas Hilfe? Ok, wir gehen bei der Zeichnung wieder Schritt für Schritt vor. Was dir sicher klar ist, dass du dir zuerst die Asymptoten überlegen solltest. Da beide Funktionen in der Form f(x) = vorliegen, lassen sich die Asymptoten direkt ablesen.

Zur Erinnerung:Die senkrechte Asymptote liegt immer bei der Definitionslücke;die Zahl hinter dem Bruch gibt die Lage der waagrechten Asymptote an.

f(x) = h(x)

Senkrechte Asymptote: x = – 1 Senkrechte Asymptote: x = – 3

Waagrechte Asymptote: y = – 1,5 Waagrechte Asymptote: y = – 2,5

Dann machst du dir Gedanken über den ungefähren Verlauf der beiden Graphen. Dazu brauchst du jeweils die Potenz n der Klammer im Nenner und das Vorzeichen der Zahl a, also des Zählers des Bruchs bzw. des ganzen Bruchs.

Hinweis:Das Vorzeichen des ganzen Bruchs muss dabei immer in den Zähler geschrieben werden, so dass das Vorzeichen von a immer dem Vorzeichen des ganzen Bruchs entspricht. Das ist vor allem dann wichtig, wenn vor dem Bruch ein Minus steht. Dann ist a nämlich negativ. In dieser Aufgabe steht aber weder bei f(x) noch bei h(x) vor dem Bruch oder im Zähler ein Minuszeichen. Daher gilt bei beiden Funktionen:

Nun betrachten wir noch jeweils die Potenz der Klammer im Nenner der Brüche. Ist n gerade oder ungerade? Bei der Funktion h(x) gibt es im Nenner der Funktionsgleichung eigentlich gar keine Klammer mit Potenz. Daher denken wir uns einfach eine Klammer mit der Potenz 1 dazu.

f(x) = h(x)

Potenz: n = 2 (gerade) Potenz: n = 1 (ungerade)

Nun kann man sich die beiden Graphen schon ganz gut vorstellen. Fertige dir dazu eine Skizze mit einem Koordinatensystem an, in das du schon ´mal die Asymptoten der beiden Funktionen gestrichelt einzeichnest. Verwende der Übersicht wegen zwei verschiedene Farben für die beiden Funktionen und ihre zugehörigen Asymptoten! Betrachte nun noch einmal die Bilder 1 bis 4, die schon in der Lösung des 1. Bsp. gezeigt wurden! (Sie sind unten gleich noch einmal zu sehen.) Welchen dieser Bilder werden die Graphen der hier vorliegenden Funktionen ähnlich sehen? Na klar! Der Graph von f(x) ähnelt dem im Bild 3 dargestellten Graph, da n gerade und a positiv ist. Der Graph von h(x) hat einen ähnlichen Verlauf wie der im Bild 1 gezeigte Graph, weil n ungerade und a positiv ist.

Hier noch einmal die Bilder 1 bis 4:

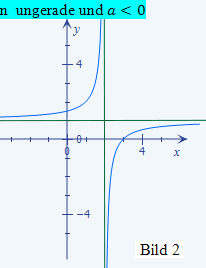
ähnlich h(x)

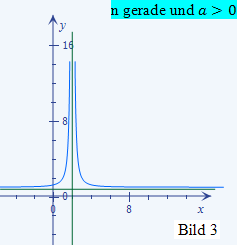
ähnlich f(x)

Jetzt kannst du dir die beiden Funktionen schon einmal grob vorstellen. Zeichne ihren Verlauf nun grob in deine Skizze, in die du bereits die Asymptoten eingezeichnet hast. Du kannst an dieser Skizze sicher erkennen, wo sich die Graphen ungefähr schneiden. Damit du den Schnittpunkt wirklich genau ablesen kannst, musst du die Graphen aber genauer zeichnen. Daher berechnest du nun einige Funktionswerte in der näheren Umgebung des Schnittpunkts. Das kannst du bestimmt alleine. (Berechne beispielsweise:f(-3), f(-2), f(-1,5), f(-0,5) und f(0), um den Graph von f(x) zeichnen zu können. Es wurden für x vor allem Werte in der Umgebung von x = -2 gewählt, da der Schnittpunkt der beiden Funktionen hier in der Nähe zu liegen scheint, was du deiner groben, vorher gezeichneten Skizze entnehmen kannst. Berechne außerdem h(-4), h(-3,5), h(-2,5), h(-2), h(-1) und vielleicht noch h(0), um den Graph von h(x) in diesem Bereich exakt zeichnen zu können. Auch hier wurden wieder Werte für x gewählt, die in der Umgebung von x = -2 liegen.)

Hinweis zur Berechnung der Funktionswerte mit einem Taschenrechner, der Wertetabellen erstellen kann:

Wähle als Startwert den kleinsten Wert von x, den du einsetzen willst, und als Endwert, den größten Wert von x, den du einsetzen möchtest. Als Step/Schrittweite △x (= Abstand der einzelnen x-Werte) nimmst du am besten △x = 0,5. Dass die Definitionslücke innerhalb dieses Bereichs liegt, stört nicht, denn der Taschenrechner wird diesen Wert einfach nicht berechnen:Bei der Definitionslücke wird er irgendetwas Ähnliches wie „math. error“ an Stelle des y-Wertes in der Wertetabelle anzeigen. Du kannst nun alle vom Taschenrechner berechneten Punkte in dein Koordinatensystem eintragen und den Graph zeichnen. (Du musst natürlich nicht alle Punkte verwenden, denn der Taschenrechner hat ja ein paar Punkte mehr berechnet, als wir eigentlich ausrechnen wollten.)

Hinweise zum Zeichnen von Hyperbeln im Koordinatensystem:

Vergiss´auch beim Zeichnen von Hyperbeln mit Wertetabelle trotzdem nicht die Asymptoten! Zeichne sie dir am besten immer gestrichelt mit ein! Du weißt, dass sich der Graph an die Asymptoten beliebig nah anschmiegt, sie aber nicht schneidet! Vorsicht:Die Punkte jeweils links und rechts der senkrechten Asymptote dürfen nicht miteinander verbunden werden! Eine Hyperbel besteht aus (mindestens) zwei getrennten Ästen! Alle Punkte, die links der senkrechten Asymptote liegen, werden miteinander zu einem Ast der Hyperbel verbunden und alle Punkte, die sich rechts von der senkrechten Asymptote befinden, werden zum zweiten Ast der Hyperbel verbunden, jedoch eben nicht die beiden Äste miteinander!

Nun hast du hoffentlich die Graphen der Funktionen f(x) = und h(x) in ein gemeinsames Koordinatensystem einigermaßen genau zeichnen können. Deine Zeichnung sollte im Prinzip aussehen wie die folgende Abbildung.

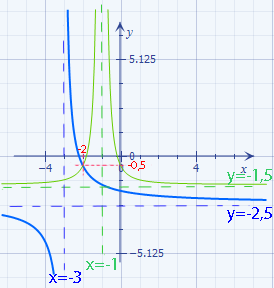
Abb.:Graphen der Funktionen f(x) = und h(x) mit ihrem Schnittpunkt (-2|-0,5)

Die x-Koordinate des Schnittpunkts der beiden Graphen lässt sich gut ablesen:x = – 2

Einen weiteren Schnittpunkt, der vielleicht außerhalb des von uns gezeichneten Ausschnitts der Funktionen liegt, kann es hier nicht geben. Das erkennst du an deiner Zeichnung, wenn du dir überlegst, wie die beiden Graphen außerhalb dieses Koordinatensystems weiter verlaufen würden. Auch wenn man das Koordinatensystem (sehr viel) größer zeichnen würde, würden sich die beiden Graphen nicht mehr schneiden. Es gibt definitiv nur einen Schnittpunkt. Daher ist die einzige Lösung unserer Bruchgleichung x = – 2.

Wir machen noch die Probe:

Hier noch einmal die Gleichung:

Probe mit x = – 2:

(wahr)

Die Probe zeigt, dass wir mit x = -2 wirklich genau die Lösung der gegebenen Bruchgleichung ermittelt haben. Damit sind wir fertig!

3. Bsp.:

Löse die folgende Gleichung graphisch!

Lösung:

Was für ein Wunder! Es liegt wieder eine Bruchgleichung vor, da die Variable x zumindest einmal im Nenner auftaucht. Die linke Seite der Gleichung enthält x im Nenner. Die rechte Seite der Gleichung enthält dagegen in diesem Beispiel kein x im Nenner;es gibt ja gar keinen Bruch auf der rechten Seite der Gleichung.

Du gehst nach dem oben beschriebenen Lösungsverfahren vor. Du siehst also die linke und die rechte Seite der Gleichung als einzelne Funktionen an, die zur Schnittpunktberechnung gleichgesetzt wurden. Die Gleichung könnte also entstanden sein beim Gleichsetzen der Funktionen f(x) = und g(x) = . Dabei handelt es sich bei f(x) um eine gebrochenrationale Funktion, d.h. um eine Hyperbel (weil x im Nenner vorkommt) und bei g(x) um eine lineare Funktion, also um eine Gerade (weil es sich um eine Funktion der Form y = mx + t handelt).

Da g(x) bereits in der Form g(x) = vorliegt, kann die Gerade mit Hilfe ihrer Steigung m und ihres y-Achsenabschnitts t schnell gezeichnet werden. Das kannst du bestimmt auch alleine. Also versuch´s doch gleich ´mal!

Du bist dir nicht mehr sicher, wie das geht? Hier noch eine kleine Hilfe:Das Steigungsdreieck wird gezeichnet, indem man sich m (die Zahl vor x in der Geradengleichung) als Bruch denkt, den Nenner nach rechts und den Zähler nach oben geht, wenn m positiv ist, bzw. nach unten, wenn m negativ ist. Das Steigungsdreieck wird immer vom y-Achsenabschnitt t aus gezeichnet.

Hast du nun versucht die Gerade selbst in ein Koordinatensystem zu zeichnen?

Ok, dann zu deiner Kontrolle hier noch einmal die genaue Vorgehensweise:

Wegen t = 3,5 musst du vom Ursprung des Koordinatensystems um 3,5 LE (Längeneinheiten z.B. cm) nach oben gehen;dort schneidet die Gerade g(x) die y-Achse. Von diesem Punkt ausgehend zeichnest du dann ein Steigungsdreieck:Da die Steigung m = ist, gehst du einfach 1 LE nach rechts und 2 LE nach unten (m ). So erhältst du einen zweiten Geradenpunkt. Durch diese beiden Punkte ist die Gerade eindeutig festgelegt;du kannst sie jetzt ganz leicht in das Koordinatensystem einzeichnen. Ausführlichere Erläuterungen dazu findest du im Kapitel Lineare Funktionen (Geraden).

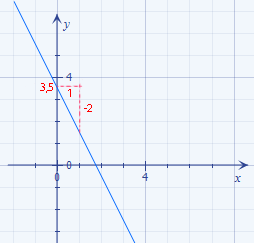
Abb.:Graph der Funktion g(x) = :Eine Gerade mit der Steigung -2 und dem y-Achsenabschnitt 3,5

Jetzt müssen wir aber auch noch die andere Funktion f(x) = in das Koordinatensystem einzeichnen. Dabei wird es etwas schwieriger. Es handelt sich um eine gebrochenrationale Funktion, die aber erfreulicherweise in der Form f(x) = vorliegt, so dass wir uns sofort eine grobe Vorstellung über den Verlauf des Graphen machen können. Liegt eine Funktion in der Form f(x) = vor, so lassen sich die Asymptoten schön ablesen. Versuche es doch selbst, die Asymptoten von f(x) = abzulesen, ohne gleich auf die folgende Lösung zu schauen!

Hier nun die Gleichungen der beiden Asymptoten von f(x) = :

Senkrechte Asymptote (≙Definitionslücke): x = 1

Waagrechte Asymptote: y = 1,5

Im Nenner des Bruchs gibt es bei f(x) eigentlich keine Klammer;man kann sich aber eine Klammer mit der Potenz 1 hinzu denken.

f(x) = f(x)

So erkennst du bestimmt, dass die Potenz n = 1 und somit ungerade ist.

Nun überlegst du dir noch, welches Vorzeichen a hier hat. Denn zusammen mit n entscheidet das Vorzeichen von a über den prinzipiellen Verlauf des Graphen. a ist genau genommen die Zahl, die im Zähler des Bruchs bei f(x) steht. Du musst dabei aber auch das Vorzeichen vor dem Bruch beachten. Das Minuszeichen, das vor dem Bruch steht, muss nämlich in den Zähler geschrieben werden.

f(x) f(x)

Für a gilt hier deshalb: a = -2

a ist hier also negativ und die Potenz n ungerade. Was bedeutet dies jetzt für den Graph von f(x)?

Im 1. Bsp. wurde bereits kurz zusammengefasst, wie der Graph einer gebrochenrationalen Funktion mit der Funktionsgleichung f(x) = (mit und n ℕ) zusammenhängt. Unten noch einmal das Bild 2, welches schon im 1. Bsp. gezeigt wurde. Es zeigt den Graph einer gebrochenrationalen Funktion mit negativem a und ungeradem n. Der Graph der Funktion f(x) muss daher so ähnlich aussehen wie der in diesem Bild dargestellte Graph. Dabei hat der Graph von f(x) natürlich die senkrechte Asymptote x = 1 und die waagrechte Asymptote y = 1,5.

• Page 1 of 2
• « Previous
• 1
• 2
• Next »